数字化信号最普遍的形式是使用等时间采样方法。也就是说数据是按恒定的速率进行采样，这个速率一般指每秒采集多少个样本点。奈奎斯特频率，fN，定义为采样速率的一半。即fN=采样速率/2。香农采样定理告诉我们，如果正在采样的信号的频率成分少于fN，那么采样将不存在混叠，采样后的信号是有效的数字化信号。而且，采样定理确保此时采样后的信号具有全部可用信息。

如果我们傅立叶分析一个信号，x(t)，那么，我们将得到这个信号在不同频率处的分量。这个过程完全是可逆的。也就是说，如果我们有信号x(t)，我们能得到X(f)。类似地，如果我们有信号X(f)，我们也能得到x(t)。有时，这个过程可以写成如下形式

x(t)↔X(f)

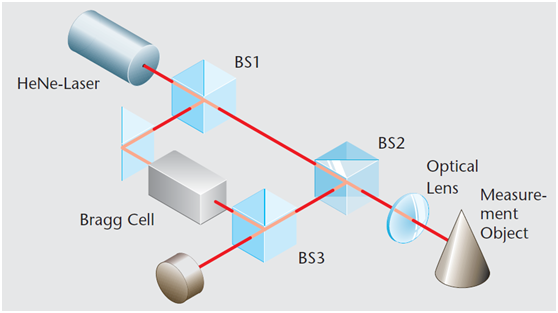
作为一个示例，考虑测试的信号由2个正弦波组成。第一个正弦波的幅值为1.0V，频率为60Hz，相位为0。第二个信号幅值为0.5V，频率为180Hz，相位为45度。我们的采样速度为每秒2048个样本点，采集2s的数据。选择采样率为2048，可确保完全压谱线采样，这虽然不是必须的，但它可避免信号泄漏。采集到的部分信号如图1所示。

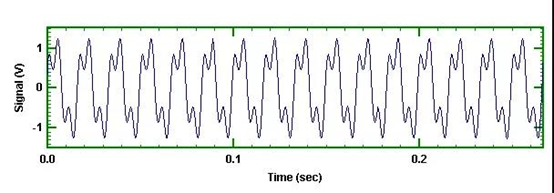
图1   2个正弦波的部分时域波形

如果我们FFT这个复合信号，那么，我们将得到其幅值和相位，如下图所示。

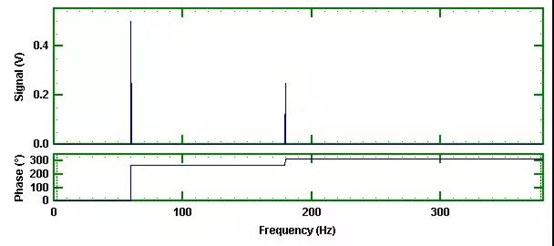
图2    2个正弦波的标准FFT

分析后的幅值分别为0.5和0.25，这是由于单边谱的幅值是真实幅值的一半，有些商业软件将会幅值加倍，在这不作加倍处理。在这个相位曲线中，我们看到在60Hz处，相位有270度的变化，在180Hz处，相位有45度的变化（从270度变化到315度）。显然45度的变化是正常的，但为什么会有270度的变化呢？它应该是0度和45度，而不是270度和315度。原因是因为傅立叶分析使用余弦，不是正弦，作为实部。一个正弦信号变成余弦信号，相位有-90度或+270度的移动。换句话说，这个信号是个余弦信号，不是一个正弦信号。

以上分析都是基本的信号分析。现在假设我们有一根旋转轴，测量这根轴的振动。旋转物体的本质特点是振动出现在转速的倍数或者约数处。譬如，如果轴的转速为3600rpm，频率为60Hz，那么，我们将会看到响应出现在这个频率的倍数处。这个倍数就是阶次。第一阶的频率等于转频，在这个例子中，第一阶是60Hz，第3阶是3*60=180Hz。阶次OR、转速R（rpm）和频率f的关系如下

f=OR*(R/60)

为什么要使用阶次？这是因为阶次对转速保持不变。第一阶次始终是转频，第二阶次始终是2倍的转频，等等。替代等时间采样，采样将按等角度方式进行，这种采样方式称为同步采样，采样与轴转速同步。假设在轴上固定了一个齿轮盘，等时间采样以时钟脉冲数进行模数转换，同步采样以每个齿上的脉冲数进行等角度采样，且速率为每圈P个样本点。

我们现有的数据是以圈为计量单位，而不是以秒为计量单位。如果采用傅立叶转换这个数据，那么我们再次得到频率类型的函数，但它的增量不再是Hz，而是阶次。分析结果给出了幅值和相位，但它们是阶次的函数，不是Hz的函数。

获得阶次不需要同步采样，因为可以使用以Hz表示的频率f，阶次数OR，和转速R之间的关系。这个过程是用FFT分析时域信号，用转速将以Hz表示的频率转换成以阶次表示的频率。对于恒定转速，这个转换是没有问题的。但是如果在整个FFT分析时间长度上，转速是变化的，那么将得到不正确的结果。也不可能以Hz表示的频率刚好完全映射成整数值的阶次。这就意味着要分组一些阶次线才能形成一个RMS值。

因此，处理旋转机械的信号优先使用同步采样，但遗憾的是，现实中执行同步采样是相当困难的。对于一些数据采集设备，是不可能进行同步采样的，像Ʃ-Δ类型的ADC必须按等时间步长进行采样。连续近似的ADC不受这个限制。这并不总是具有现实意义，因为通常很难得到一个可靠的每转一个脉冲的转速，更别说每转N个脉冲了。

解决方案是使用信号处理去数字化重采样数据。再次，我们注意到香农采样定理的含义，也就是说我们采样的速率至少要两倍于出现的最高频率，这样我们才有信号的所有信息。使用正确的信号处理算法，我们可以将原始的等时间采样得到的数据重采样成等角度方式的数据。不涉及这方面的理论和相关方程，只需要注意的是重采样是基于（sinx/x）函数。这个函数称为sinc函数。使用这个重采样算法只是去改变采样速率。当重采样到等角度方式时，显然每转一个脉冲的转速信号是需要的，这个转速信号将提供时间与总“角度”之间的关系。

使用每转一个脉冲的转速信号将常规的时间序列信号转换成同步的时间序列。我们对之前图1所示的复合正弦信号进行重采样。一个转速信号匹配60Hz的频率分量，第一阶次等于60Hz的信号。每圈采样32个数据点。一个新的同步信号如图3所示，看起来与之前的等时间采样数据相同，除了横轴现在是用总的角度来表示之外。

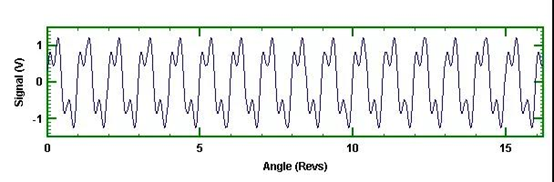
图3    同步采样两个正弦波

同步采样的信号的FFT结果如图4所示。

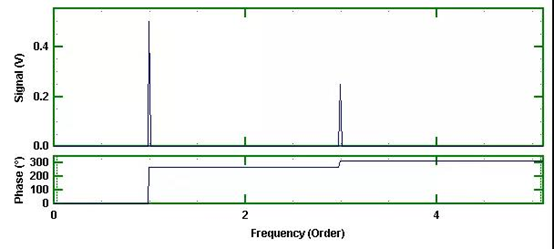
图4 同步信号的FFT结果

这跟之前的等时间采样的FFT结果相同，与预期一样，除了横轴现在是用阶次标识，不再是Hz之外。两个响应刚好位于1阶次和3阶次处，与预期相同。

更复杂的信号如图5所示，这是车辆稳态运行下的信号。显然在这个信号中存在“拍”现象。车速不稳定，因此，如果在时域分析这个信号，那么幅值将拖尾到一些频率成分上。

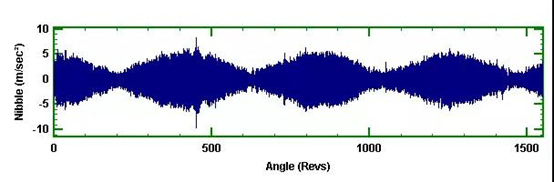
图5  同步采样汽车振动信号

图6表明阶次分析给出了非常清晰的结果，能量主要集中在第一阶次，还有一些边频带，在第二和第三阶次上也存在少量贡献。

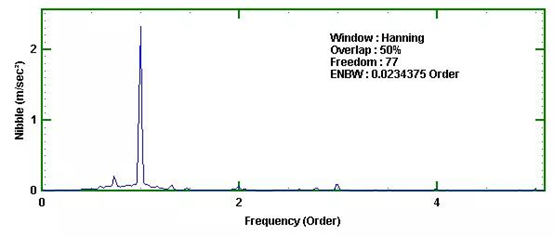
图6 汽车信号的阶次分析

更能揭示实情的信号是分析简单的正弦扫频信号，如图7所示。

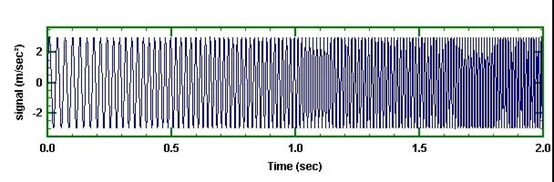
图7  正弦扫频从30Hz到100Hz

如果我们分析这个信号，按常规的时间历程来分析，那么，我们将得到30Hz到100Hz的频谱如图8所示。

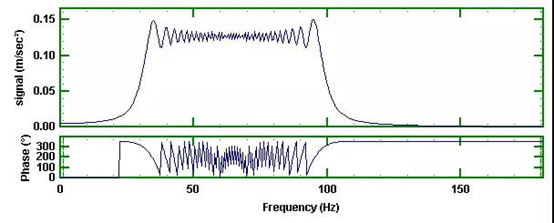
图8  正弦扫频的FFT结果

现在如果我们同步采样这个正弦扫频信号，按每转一个脉冲进行，然后进行频域分析，得到同步的信号如图9所示。

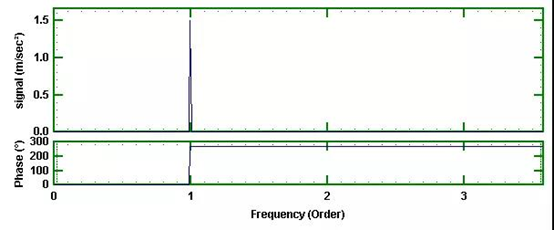
图9  同步采样的正弦扫频

整个信号完全集中在第一阶次，幅值是半幅值，相位跳动270度。如果我们观察同步采样的信号，如图10所示，那么“正弦扫频”的信号现在恰好是一个“单频正弦波”。我们每转采样的数据点不变，改变的只是速度。

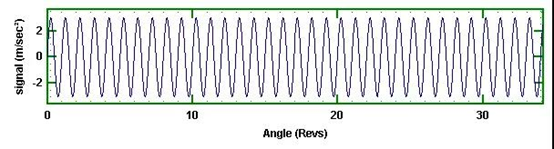
图10  同步正弦扫频信号的阶次分析

在同步采样的同时，会另外保留时间-角度曲线信号，因此，没有信息丢失。这个信号如图11所示。

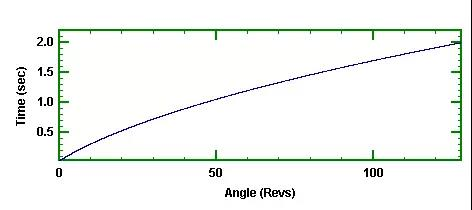
图11    时间-角度信号

因为扫频的速率是个常数，因此，时间-角度曲线关系是时间=K*sqrt(角度)。

文章来源：模态空间